What is the Difference between Low & High Cycle Fatigue?

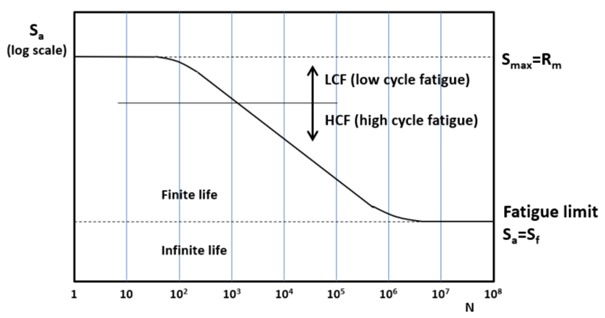
The difference between low cycle fatigue (LCF) and high cycle fatigue (HCF) has to do with the deformations. LCF is characterized by repeated plastic deformation (i.e. in each cycle), whereas HCF is characterized by elastic deformation. The number of cycles to failure is low for LCF and high for HCF, hence the terms low and high cycle fatigue.
Transition between LCF and HCF is determined by the stress level, i.e. transition between plastic and elastic deformations. That implies that there is no fixed transition life, e.g. 10³, but that transition life depends on the ductility of the material.

See also: Using the Low Cycle Fatigue approach when Kt * nominal stress exceeds the yield strength: a fundamental mistake!